Probabilidad

Contenido

• Definición de probabilidad.
• Definciones de términos.
• ¿Cómo se calculan probabilidades?
• Regla de la suma de probabilidades
• Regla de la probabilidad condicional
• Fórmulas para el cálculo de probabilidades

Definición de probabilidad.

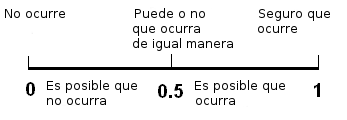
La probabilidad es una medida de la incertidumbre.

La probabilidad mide la posibilidad con la cual pueda ocurrir un evento al realizar un experimento.

Si denotamos $A$ por el evento, entonces $P(A)$ se asocia a la probabilidad de ese evento.

Por ejemplo si examinamos el estado del tiempo para Medellín y nos dice que a las 6:00 pm de hoy hay una probabilidad del 35% de que llueva entonces escribimos:

$$\begin{aligned} A & : \textrm{Llover en Medellín a las 6:00 pm del día de hoy.} \\ P(A) & : \textrm{Probabilidad de que lloverá en Medellín a las 6:00 pm el día de hoy.}\\ P(A) & = 0.35 \end{aligned}$$

La probabilidad está definida sólo para números reales entre 0 y 1, es decir $0 \le P(A) \le 1$.

Definciones de términos.

• Espacio Muestral: Es el conjunto de todas los posibles resultados de un experimento o de un proceso aleatorio. Se suele denotar por $S$.

• Evento: Es una subconjunto específico de resultados de un experimento. Es un subconjunto del espacio muestral. Se utilizan letras mayúsculas para denotarlo ($A, B, C, ...$).

¿Cómo se calculan probabilidades?

• Fórmula frecuentista: Si todos los posibles resultados tienen la misma posibilidad de ocurrir, entonces:

$$\begin{aligned} P(E) = \frac{\textrm{Total de resultados favorables a E}}{\textrm{Total de resultados del espacio muestral S}} \end{aligned}$$

• Ejemplo 1: Definimos el experimento como elegir al azar una persona de un grupo de 11 personas de las cuales sólo siete saben la definición de probabilidad.

  ¿Cuál es la probabilidad de que esa persona que elijamos al azar sepa la definción de probabilidad?

  $$S = \{\textrm{sabe, sabe, sabe, sabe, sabe, sabe, sabe, no sabe, no sabe, no sabe, sabe}\}$$ $$E: \textrm{Elegir una persona que sabe la definición de probabilidad}$$ $$E= \{\textrm{sabe, sabe, sabe, sabe, sabe, sabe, sabe, sabe} \}$$

  Entonces:

  $$\begin{aligned} P(E) & = \frac{\textrm{Total de personas que sabe la definición de probabilidad}}{\textrm{Total de personas del grupo}} = \frac{8}{11} = 0.727272... \\ P(E) & = 0.727272... \end{aligned}$$

• Ejempo 2: ¿Cuál es la probabilidad de que tomando dos personas ambas sepan la definición de probabilidad?

  En este caso el espacio muestral es el número total de parejas que puedo formar con las once personas. Utilizando la fórmula de calcular de un grupo de $n$ individuos formar grupos de $r$ individuos:

  $$\begin{aligned} {n \choose r} = \frac{n!}{r!(n-r)!} \end{aligned}$$

  Donde $x!$ es el factorial de un número que se define como $x!=x \cdot (x-1) \cdots 3 \cdot 2 \cdot 1$. Por ejemplo $4!$ es $4 \cdot 3 \cdot 2 \cdot 1 = 24$ es decir $4!=24$. Por definición $0!=1$.

  Si se tiene un grupo de $n$ personas de las cuales $c_1$ son de una clase, y $c_2$ son de otra clase y además $n=c_1 + c_2$, entonces el número de grupos que podemos formar de las cuales tomamos $r_1$ de la clase $c_1$ y $r_2$ de la clase $c_2$, se tiene que la fórmula es:

  $$\begin{aligned} {n \choose {r_1 \quad r_2}} = {c_1 \choose r_1} \cdot {c_2 \choose r_1} \end{aligned}$$

  Esta fórmula también se puede extender para cuando se tengan más de dos clases.

  En nuestro ejemplo el número total de grupos de dos personas que se pueden formar del grupo de once personas es:

  $$\begin{aligned} {11 \choose 2} & = \frac{11!}{2!(11-2)!} = \frac{11!}{2! \cdot 9!} = \frac{11 \cdot 10 \cdot 9! }{ 2 \cdot 9!} = \frac{11 \cdot 10 }{ 2} = 11 \cdot 5 = 55\\ {11 \choose 2} & = 55 \end{aligned}$$

  Ahora calculemos cuántas grupos de dos personas podemos formar que las dos tengan conocimiento de la definción de probabilidad y cero de los que no tengan conocimiento de la definción de la probabilidad.

  $$\begin{aligned} {11 \choose {2 \quad 0}} & = {8 \choose 2} {3 \choose 0} = \frac{8!}{2!(8-2)!} \cdot \frac{3!}{0!(3-0)!} = = \frac{8!}{2! \cdot 6!} \cdot \frac{3!}{3!} = \frac{8 \cdot 7 }{ 2} \cdot 1 = 4 \cdot 7 = 28\\ {11 \choose {2 \quad 0}} & = 28 \end{aligned}$$

  Entonces de acuerdo a la fórmula frecuentista tenemos que:

  $$\begin{aligned} P(E) & = \frac{\textrm{Total de grupos donde ambas personas saben la definición de probabilidad}}{\textrm{Total de grupos de dos personas}} = \frac{28}{55} \approx 0.51\\ P(E) & = \frac{28}{55} \approx 0.51 \end{aligned}$$

  ¿Cuál será la probabilidad de que si se toma un grupo de dos personas la una sepa la definición de probabilidad y la otra no la sepa?

  Ejemplo 3: Si un carro nuevo está disponible en tres colores (rojo, azul y gris) con posibilidad de dos motores diferentes (M1 y M2). Si selecciono a azar dos combinaciones, ¿cuál es la probabilidad de que escoja un carro gris con el motor M2 o un carro azul con el motor M1?

  En este caso debo contar el número de posibles combinaciones, que son tres tipos colores y por cada color, dos tipos de motores, luego el total de posibilidades son $3 \times 2$.

  El evento que me están preguntado tiene dos combinaciones: color gris con motor M2 o motor azul con motor M1. $E = \{ \textrm{gris-M2}, \textrm{azul-M1} \}$.

  Siguiendo la regla de las probabilidades tenemos que

  $$\begin{aligned} P(E) = \frac{\textrm{Total de resultados favorables a E}}{\textrm{Total de resultados del espacio muestral S}} = \frac{2}{6} = \frac{1}{3} \approx 0.33 \end{aligned}$$

  Es decir que la probabilidad de que un carro elejido al azar sea un carro gris con motor M2 o un carro azul con motor M1 es de aproximadamente 0.33.

Regla de la suma de probabilidades

• Si los eventos son mutuamente excluyentes. Es decir que NO se pueden suceder los dos al mismo tiempo.

  $$P(A \cup B) = P(A) + P(B)$$

• Si los eventos no son mutuamente excluyentes, entonces la fórmula es:

  $$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$

  Note que si A es un evento y A’ es su complemento o su negación entonces son eventos mutuamente excluyentes y además $P(A) = 1- P(A')$, porque $P(A \cup A') = 1$ porque la probabilidad de que los dos eventos unidos ocurran es un evento seguro, porque necesariamente ha ocurrido alguno de los dos.

  Por ejemplo definamos el evento $L:$ Llueve el día de mañana, entonces $L'$ será su complemento y se definirá como $L':$ No llueve el día de mañana. Entonces el evento $L \cup L'$ es el evento que llueve o no llueve en el día de mañana, entonces $P(L \cup L')=1$, porque es seguro que alguno de los dos ocurra. Además son mutuamente excluyentes porque sólo puede ocurrir uno de los dos eventos, no pueden ocurrir los dos al mismo tiempo, es decir $P(L \cap L')=0$, por que es imposible que al mismo tiempo llueva y no llueva mañana. Entonces si por ejemplo la probabilidad de que mañana llueva es del $P(L)=0.2$, entonces la probabilidad de que no llueva mañana es de $P(L')=1-P(L)=1-0.2=0.8$.

• Ejemplos:

  • Se sabe que en la UNAC el 60% de los estudiantes estudian inglés, y el 20% estudian portugués. Por otro lado se sabe que los que estudian tanto inglés como portugués al mismo tiempo son el 5%. ¿Cuál es la probabilidad de que al tomar un estudiante al azar este estudiando algún idioma ya sea inglés, portugués o ambos?

    En este caso definamos el evento los eventos $I$:Estudia inglés, $P$: Estudia portugués, luego se está preguntando por $P(I \cup P)$. De acuerdo al enunciado $P(I)=0.6$, $P(P)=0.2$ y $P(I \cap P) = 0.05$.

    Debido a que no son eventos excluyentes entonces se utilizará la fórmula:

    $$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$

    Entonces para nuestro caso tenemos:

    $$\begin{aligned} P(I \cup P) & = P(I) + P(P) - P(I \cap P) = 0.6 + 0.2 - 0.05 = 0.75 \\ P(I \cup P) & = 0.75 \end{aligned}$$

    Luego la probabilidad de encontrar al azar un estudiante que al menos esté estudiando un idioma en UNAC es de $0.75$.

  • Se sabe que en la UNAC el porcentaje de estudiantes que son de la costa es del 30%, el porcentaje de los llaneros es del 25%, el porcentaje de santandereanos es del 20% y el del Valle son el 10% y del resto del país el 15%. ¿Cuál es la probabilidad de que al tomar un estudiante al azar este sea de la costa o del Valle?

    En este caso definimos los eventos $C:$Ser de La Costa, $L$: Ser del Llano, $S$: Ser de Santander, $V:$ Ser del Valle y $R:$ resto del país. Entonces la pregunta es $P(C \cup V)$.

    Como los eventos son mutuamente excluyentes entonces:

    $$\begin{aligned} P(C \cup V) & = P(C) + P(V) = 0.3 + 0.25 = 0.55 \\ P(C \cup V) & = 0.55 \end{aligned}$$

    Luego el probabilidad de encontrar al azar un estudiante que sea de La Costa o del Valle es de $0.55$.

  • Se ha observado que la distribución de porcentajes de acuerdo al número de salarios mínimos mensuales legales vigentes (SMMLV) ganan los colombianos es:

    Grupo	Ingresos en SMMLV	Porcentaje
    1	0	7.4%
    2	(0,0.5]	21.9%
    3	(0.5,1]	25.8%
    4	(1, 1.5]	22.7%
    5	(1.5, $\infty$)	22.2%
    Total		100%

    • ¿Qué probabilidad existe que una persona elegida al azar gane más de 1 SMMLV?
    • ¿Qué probabilidad existe que una persona elegida al azar gane medio o menos SMMLV?
    • ¿Qué probabilidad existe que una persona elegida al azar gane un SMMLV o menos?
    • ¿Qué probabilidad existe que una persona elegida al azar gane algo de salario (distinto de cero)?

    Definamos los eventos $A_1:$ Ganar cero SMMLV, $A_2:$ Ganar más que cero y medio SMMLV, $A_3:$ Ganar más de medio SMMLV y un SMMLV, $A_4:$ Ganar más de uno SMMLV y uno y medio SMMLV y $A_5:$ Ganar más de uno y medio SMMLV.

    En este caso las probabilidades se distribuyen así $P(A_1)=0.074$, $P(A_2)=0.219$, $P(A_3)=0.258$, $P(A_4)=0.227$ y $P(A_5)=0.222$

    Notemos que los eventos así definidos son mutuamente excluyentes así que se puede verificar que:

    $$P(A_1 \cup A_2 \cup A_3 \cup A_4 \cup A_5) = P(A_1) + P(A_2) + P(A_3)+ P(A_4)+ P(A_5) = 1$$

    • Para este caso se pregunta $P(A_4 \cup A_5)$. Dado que los eventos son mutuamente excluyentes, entonces $P(A_4 \cup A_5) = P(A_4) + P(A_5) = 0.227 + 0.222 = 0.449$. Es decir que el 44.9% de las personas ganan más de un SMMLV.

    • Para este caso se pregunta $P(A_1 \cup A_2)$. De nuevo los eventos son mutuamente excluyentes, entonces $P(A_1 \cup A_2) = P(A_1) + P(A_2) = 0.074 + 0.219 = 0.293$. Es decir que el 29.3% de las personas ganan medio o menos SMMLV.

    • En este caso se pregunta por $P(A_1 \cup A_2 \cup A_3)$. Como los eventos son mutuamente excluyentes, entonces $P(A_1 \cup A_2 \cup A_3) = P(A_1)+ P(A_2) + P(A_3) = 0.074 + 0.219 + 0.258 = 551$. Es decir que el 55.1% de las personas ganan un SMMLV o menos. Es decir la mayoría de las personas ganan en Colombia un SMMLV o menos.

    • Se puede resolver este punto similar a los anteriores, pero es más facil realizar el siguiente cálculo. Dado que se tiene $P(A_1)$, lo que nos están preguntando es $P(A_1')$ y se puede calcular como: $P(A_1') = 1 - P(A_1) = 1 - 0.074 = 0.926$. Es decir que el 92.6% de los colombianos reciben algún tipo de ingreso.

  • En una comunidad se sabe que el porcentaje que consumen un alimentos altos en grasa o consumen alimentos altos en azúcar o ambos tipos de alimentos es del 80%. También se sabe que los que consumen altos contenidos en grasa es el 50% y los que consumen altos contenidos de azúcar es del 60%. ¿Qué porcentaje de personas consumen simultáneamente tanto altos contenidos de grasa y altos contenidos de azúcar?

    En este caso se tiene que $G:$ Consume alimentos altos en grasa, $A:$ Consumen alimentos con alto contenido de azúcar. Además se menciona que $P(G) = 0.50$, $P(A) = 0.60$, y $P(G \cup A)=0.8$. Lo que se pregunta por lo tanto es $P(G \cap A)$.

    Dado que los eventos no son mutuamente excluyentes se despejará de la fórmula:

    $$P(G \cup A) = P(G) + P(A) - P(G \cap A)$$

    el valor de $P(G \cap A)$. Es decir:

    $$P(G \cap A) = P(G) + P(A) - P(G \cup A)$$

    Entonces el resultado será:

    $$P(G \cap A) = P(G) + P(A) - P(G \cup A) = 0.5 + 0.6 - 0.8 = 0.3$$

    Entonces el porcentaje que consume altos contenidos de grasa y simultáneamente altos contenidos de azúcar es del 30%.

  • Las distribuciones de las probabilidades se puede hacer también mediante una fórmula (es más convinientes y es muy usual). Por ejemplo supongamos que $X$ es la cantidad de inversión que usted realiza en la bolsa de valores y sólo está permitido invertir, 6, 7, 8 y 9 millones de pesos, y únicamente esas cantidades de manera excluyente. Las probabilidades de obtener una ganancia está dada por la siguiente fórmula:

    $$P(X=x) = \frac{x-5}{10}, x=6,7,8,9 \quad \textrm{Donde } X \textrm{ es el dinero invertido en millones de pesos}.$$

    Es decir si queremos saber con qué probabilidad se gana en la inversión al invertir ocho (8) millones de pesos entonces reemplazamos en la fórmula y obtenemos:

    $$P(X=8) = \frac{8-5}{10} = \frac{3}{10} = 0.3$$

    Se puede verificar que $P(X=6 \cup X=7 \cup X=8 \cup X=9)$ $= P(X=6) + P(X=7) + P(X=8) + P(X=9)$ $= 1$, debido a que son evento mutuamente excluyentes.

    Se nos puede preguntar ¿Que opción de inversión tiene mayor probabilidad de ganar? ¿Invertir 6, 7 u 8 millones, en comparación con sólo invertir 9 millones?

    La primera opción es $P(X=7 \cup X=8)$ y la segunda opción es $P(X=9)$.

    Para la primera opción:

    $$P(X=7 \cup X=8) = P(X=7) + P(X=8) = 0.2 + 0.3 = 0.5$$

    La segunda opción de inversión es:

    $$P(X = 9) = 0.4$$

    Luego es mejor invertir ya sea 7 u 8 millones, que invertir sólo 9 millones.

Regla de la probabilidad condicional

• Si se quiere calcular la probabilidad de un evento dado que ya sucedió otro evento se calcula como:

  $$P(A / B) = \frac{P(A \cap B)}{P(B)}$$
• Ejemplo:

  • El porcentaje de personas que son deshonestos y que no adquieren un buen trabajo es del 20% y por otro lado el porcentaje en general de personas deshonestas se estima en un 60%. ¿Cuál es el porcentaje de personas que no adquieren un buen trabajo dado que son deshonestas?

    En este caso $D:$ La persona es deshonesta, $N:$ No tiene un buen trabajo, entonces los datos que nos suministran son $P(D)=0.6$ y $P(N \cap D)=0.2$, se pregunta entonces por $P(N/D)$.

    Al usar la fórmula tenemos que:

    $$P(N / D) = \frac{P(N \cap D)}{P(D)} = \frac{0.2}{0.6} = \frac{1}{3} \approx 0.33$$

    Luego el procentaje de personas que dado que son deshonestas, no adquieren un buen trabajo es aproximadamente del 33%.

• Si dos eventos son independientes (el uno no influye en el otro) se tiene que:

  $$P(A \cap B) = P(A) P(B)$$

• Como consecuencia tenemos que si los eventos son independientes, es decir que ninguno dependa del otro entonces:

  $$P(A / B) = P(A)$$
• Ejemplo:

  • Un contador experto en auditoría tiene una probabilidad del 0.9 de encontrar un error en un estado de cuenta, mientras que un contador recién graduado y sin mucha experiencia tiene una probabilidad de encontrar un error en un estado de cuenta de 0.2. La probabilidad de que ambos encuentren un error al revisar el mismo estado de cuenta es de 0.18. ¿Los dos eventos son independientes?

    En este caso consideremos $E:$ El contador experto encuentra un error en un estado de cuenta, y $R:$ El contador recién graduado y sin mucha experiencia encuentra un error en un estado de cuenta. Entonces de acuerdo a los datos tenemos que $P(E)=0.9$, $P(R)=0.2$ y $P(E \cap R) = 0.18$.

    Si los eventos son independientes entonces de deberá cumplir que:

    $$P(E \cap R) = P(E) P(R) = 0.9 \cdot 0.2 = 0.18$$

    Entonces observamos que es igual a $P(E \cap R)$ dado como dato, por lo tanto los eventos son independientes.

    Otra manera de resolver la situación es calcular $P(E/R)$, es decir, dado que el contador recién graduado ha encontrado el error en el estado de cuenta, ¿cuál es la probabilida de que el contador experto también lo haga?

    Entonces utilizaremos la fórmula de la probabilidad condicional

    $$P(E / R) = \frac{P(E \cap R)}{P(R)} = \frac{0.18}{0.2} = 0.9$$

    Es claro que $P(E/R) = P(E) = 0.9$, es decir que el hecho que uno de los contadores haya encontrado un error en el estado de cuenta es independiente que el otro lo haya encontrado o no.

Pero si los eventos no son independientes entonces

$$P(A \cap B) = P(A / B)P(B) = P(B / A)P(A)$$

• Ejemplos:

  • La probabilidad de pasar un examen de 0.8. Pero la probabilidad de que un estudiante estudie y también pase el examen es de 0.75. ¿Cúal es la probabilidad de que el estudiante haya estudiado dado que pasó el examen?

    En este caso tenemos los eventos $G:$ Pasar o ganar el examen, $E:$ estudiar para el examen. Entonces $P(G)=0.8$ y $P(G \cap E)=0.75$, se nos pide $P(E/G)$.

    $$P(E / G) = \frac{P(G \cap E)}{P(G)} = \frac{0.75}{0.8} = 0.9375 \approx 0.94$$

    Por lo tanto la probabilidad que el estudiante haya estudiado dado que ganó el examen es de 0.94.

  • Se sabe que el porcentaje de estudiantes residentes en la UNAC es el 70% de los estudiantes, y también se ha establecido que si el estudiante es residente, la probabilidad de que tenga un promedio mayor a 3.8 es de 80%. ¿Cuál es el porcentaje de estudiantes que son residentes y tienen un promedio mayor de 3.8?

    Definimos a $R:$ El estudiante es residente, $A:$ El estudiante tiene un promedio alto (mayor a 3.8). Luego tenemos que $P(R)=0.7$ y $P(A/R)=0.8$. Se pregunta por $P(R \cap A)$.

    Al utilizar la fórmula de la probabilidad condicional:

    $$P(A/R) = \frac{P(A \cap R)}{P(R)}$$

    se tiene que se conoce $P(A/R)$ y también $P(R)$, entonces despejamos a $P(A \cap R)$.

    $$P(A \cap R) = P(A/R)P(R) = 0.8 \cdot 0.7 = 0.56$$

    Por lo tanto el porcentaje de estudiantes que son residentes y tienen un promedio mayor a 3.8 es de 56%

  • Se tiene que una prueba para verificar si alguien padece de diabetes no es cien por ciento segura y se ha determinado que tiene una probabilidad de indicar diabetes cuando realmente tiene diabetes es del 0.99. También se sabe que la probabilidad de indicar que no tiene diabetes cuando realmente no padece esa enfermedad es de 0.95. Por otro lado se tiene que en una comunidad el 20% de las personas son diabéticas, entonces si tomamos una persona al azar, la probabilidad de que sea diabética es de 0.2. Se quiere determinar cuál es la probabilidad de que una persona tomada al azar sea diabética dado que la prueba dió positiva para la enfermedad.

    En este caso definamos los eventos: $D:$ La persona es diabética, $R:$ El resultado de la prueba es positivo para diabetes. Entonces de acuerdo a los datos $P(R/D)=0.99$, $P(R'/D')=0.95$, $P(D) = 0.2$ Y lo que se pregunta es que $P(D/R)$.

    Entonces si partimos de la fórmula de la probabilidad condicional entonces se tiene que:

    $$P(D / R) = \frac{P(D \cap R)}{P(R)}$$

    En este caso no se conoce ni $P(D \cap R)$ ni $P(R)$. Pero utilizando la misma fórmula podemos hallar $P(D \cap R)$ de la siguiente manera:

    $$P(R / D) = \frac{P(R \cap D)}{P(D)} = \frac{P(D \cap R)}{P(D)}$$

    Ya que $P(D \cap R) = P(R \cap D)$ entonces despejemos de la anterior fórmula $P(D \cap R)$, entonces:

    $$P(D \cap R) = P(R/D)P(D) = 0.99 \cdot 0.2 = 0.198$$

    Sin embargo todavía queda por hallar $P(R)$, para este efecto consideremos que toda la población esta sólo en dos posibles estados $D$ y $D'$ y además son eventos mutuamente excluyentes, es más, también podemos considerar que $D \cap R$ y $D' \cap R$ también son dos eventos mutuamente excluyentes, que se definirías como: $D \cap R:$ La persona es diabética y le dió positivo la prueba y $D' \cap R:$ La persona no es diabética y la prueba le dió positiva (por que la prueba no es cien por ciento segura).

    Note que $R = (D \cap R) \cup (D' \cap R)$, y además son dos eventos mutuamente excluyentes $(D \cap R)$ y $(D' \cap R)$, como se muestra en el siguiente diagrama:

    

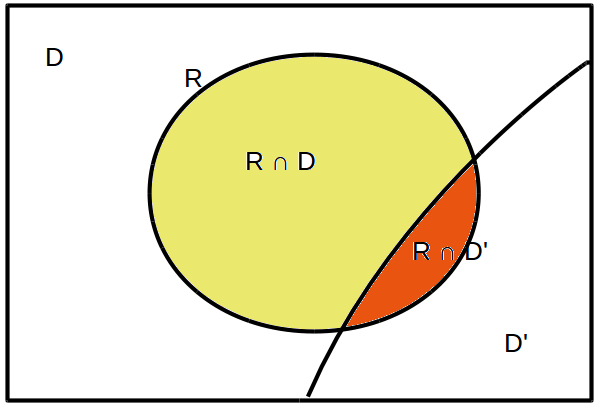
    Ya hemos calculado $P(D \cap R)$, pero falta $P(D' \cap R)$.

    Utilizaremos de nuevo la fórmula de probabilidad condicional de la siguiente manera:

    $$P(R/D') = \frac{P(R \cap D')}{P(D')}$$

    En este caso obtenemos a $P(D')$ de $P(D') = 1-P(D)$, y también a $P(R/D') = 1 - P(R'/D')$, porque tenemos tanto a $P(D)=0.2$, como a $=P(R'/D')=0.95$, entonces $P(D') = 0.8$ y $P(R/D') = 0.05$, despejando a $P(R \cap D')$ que es lo mismo que $P(D' \cap R)$, entonces:

    $$P(D' \cap R) = P(R/D') P(D') = 0.05 \cdot 0.8 = 0.04$$

    Recordemos que $(D \cap R)$ y $(D' \cap R)$ son dos eventos mutuamente excluyentes entonces:

    $$P(R) = P((D \cap R) \cup (D' \cap R)) = P(D \cap R) + P(D' \cap R) = 0.198 + 0.04 = 0.238$$

    Retomando la fórmula inicial tenemos que:

    $$P(D / R) = \frac{P(D \cap R)}{P(R)} = \frac{0.198}{0.238} = 0.8319328$$

    Entonces la probabilidad de que una persona elegida al azar tenga diabetes, dado que el resultado de la prueba dió positivo para diabetes es de aproximadamente 0.83.

Fórmulas para el cálculo de probabilidades

Fórmulas de probabilidad